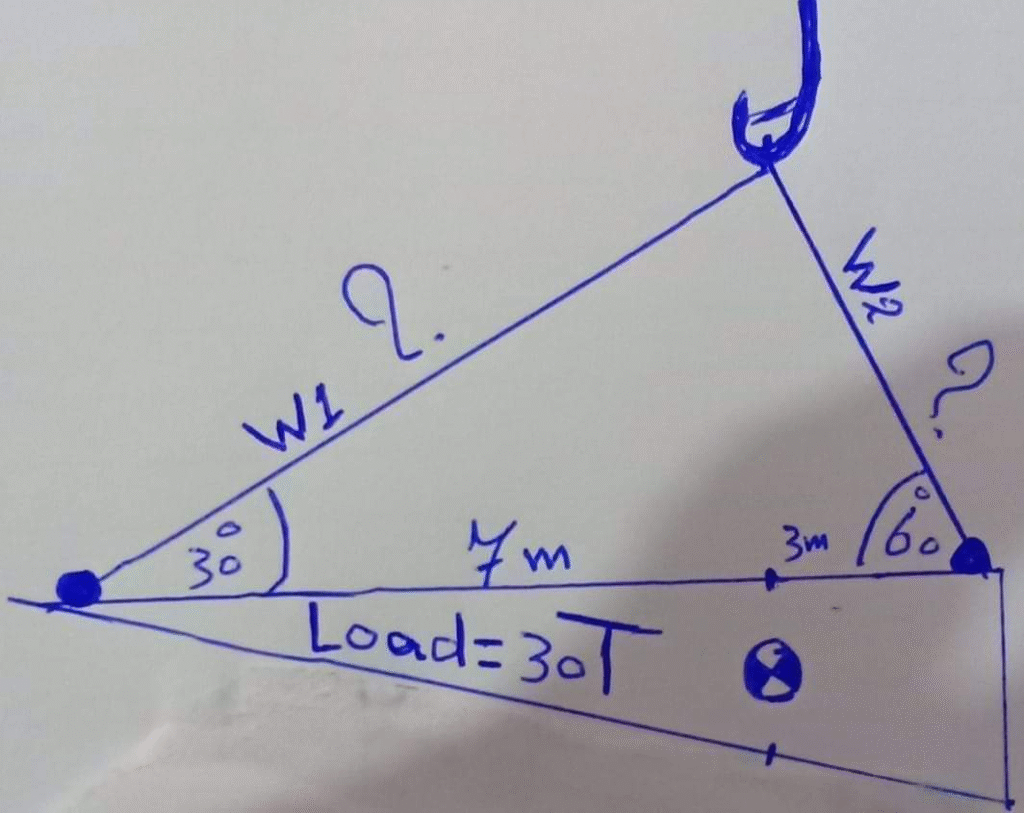
تعتبر عملية حساب قوى الشد (Calculation of Tension Forces) على أسلاك الرفع (Lifting Wires) أو الحبال (Slings) من الخطوات الجوهرية لضمان سلامة عملية النقل (Lifting Operation) وسلامة الحمولة (Load Integrity). يُطرح التساؤل الفني (Technical Inquiry) حول مقدار قوة الشد (Magnitude of Tension Force) التي يتحملها كل سلك.
الصيغة الرياضية الأساسية (The Fundamental Mathematical Formula)
تُحتسب قوة الشد (Tension Force, T) المؤثرة على أي سلك رفع في حالة الحمولة الموزعة بشكل غير متماثل (Asymmetrically Distributed Load) وفقًا للمعادلة التالية:
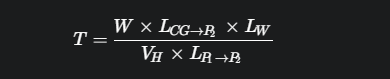
حيث:
- T: قوة الشد (Tension Force) على السلك الأول (W1).
- W: وزن الطرد (Load Weight) أو وزن الحمولة (Load Mass).
- LCG→P2: المسافة الأفقية (Horizontal Distance) من مركز الثقل (Center of Gravity, CG) إلى نقطة تثبيت السلك الثاني (Anchoring Point P2).
- LW: الطول الفعلي للسلك (Actual Wire Length).
- VH: المسافة الرأسية (Vertical Distance) من نقطة الرفع (The Hook Level) إلى خط تثبيت الأسلاك (The Anchoring Line).
- LP1→P2: المسافة بين نقطتي التثبيت (Distance Between the Two Anchoring Points, P1 and P2).
ملاحظة منهجية (Methodological Note): في حالة الرفع بزوايا مائلة (Angled Lifting), يتم اختصار وتبسيط الصيغة عادةً باستخدام نسبة طول السلك إلى الارتفاع الرأسي (Ratio of Wire Length to Vertical Height) والتي تُعبر عنها بـمقلوب جيب الزاوية (The Inverse of the Sine of the Angle, 1/sin(θ)) بين السلك والسطح الأفقي.
تطبيق عملي (Practical Application)
بتطبيق المعادلة على الشكل المراد حساب قوى الشد (Tension Forces) على أسلاكه (W1 و W2)، وكانت وزن الحمولة (Load Weight) W=30 طن:
1. حساب الشد على السلك الأول (W1):
يُحسب قوة الشد (T1) على السلك الأول (W1) بالاعتماد على ذراع مركز الثقل (Lever Arm) المعاكسة وزاوية ميله (Angle of Inclination):

2. حساب الشد على السلك الثاني (W2):
يُحسب قوة الشد (T2) على السلك الثاني (W2) بالاعتماد على ذراع مركز الثقل المعاكسة وزاوية ميله:

اعتبارات تحليلية هامة (Critical Analytical Considerations)
لضمان الدقة والاحترافية، يجب أخذ الملاحظات التالية في الحسبان:
- علاقة الزاوية بالشد (Angle-Tension Relationship): تتأثر قوة الشد (Tension Force) على أسلاك الرفع بعلاقة عكسية (Inverse Relationship) مع جيب الزاوية (sin) بين السلك والسطح الأفقي (Horizontal Plane) لنقطة التثبيت. كلما كانت الزاوية أصغر (Closer to the Horizontal), زادت قوة الشد بشكل كبير.
- علاقة المسافة بالشد (Distance-Tension Relationship): تتأثر قوة الشد (Tension Force) على أي سلك بعلاقة عكسية (Inverse Relationship) مع المسافة الأفقية (Horizontal Distance) بين نقطة تثبيته (Its Anchoring Point) ومركز ثقل الحمولة (Load’s Center of Gravity, CG). أي أن السلك الأقرب لمركز الثقل هو الأقل تحملاً للشد، بشرط تساوي الزوايا. أما في حالة التوزيع غير المتماثل (Asymmetric Distribution) كما في المثال، فإن السلك الواقع على الجانب ذي المسافة الأبعد (Longer Horizontal Distance) عن مركز الثقل هو الذي يتحمل أقصى قوة شد (Maximum Tension Force).
